Bevor wir darauf eingehen, zuerst eine kurze Einführung in die Theorie kombinatorischer Designs.
Lotto Designs sind eine Verallgemeinerung der t-Designs bzw. Blockpläne, die wir als bekannt voraussetzen. Als Zwischenschritt definieren wir eine andere Verallgemeinerung des t-Designs, nämlich das Covering Design in Anlehnung an [2] wie folgt:
Es sei ![]() . Ein t-(v,k,
. Ein t-(v,k,![]() ) Covering Design
ist ein Paar (V,
) Covering Design
ist ein Paar (V,![]() ) mit V als eine Menge von v Elementen
(den Punkten) und
) mit V als eine Menge von v Elementen
(den Punkten) und ![]() einem Mengensystem von k-Untermengen von V
(den sogenannten Blöcken) mit folgender Eigenschaft: Jede der insgesamt
einem Mengensystem von k-Untermengen von V
(den sogenannten Blöcken) mit folgender Eigenschaft: Jede der insgesamt
![]() t-Untermengen von V muss in mindestens
t-Untermengen von V muss in mindestens ![]() Blöcken
enthalten sein. Die minimale Blockzahl
Blöcken
enthalten sein. Die minimale Blockzahl
![]() bezeichnet
die kleinstmögliche Zahl solcher Blöcke.
bezeichnet
die kleinstmögliche Zahl solcher Blöcke.
Beispiel 2: Wir betrachten das 3-(8,6,1)-Covering Design, bzw.
wegen ![]() kürzer geschrieben das (8,6,3)-Covering Design, mit den
Blöcken:
kürzer geschrieben das (8,6,3)-Covering Design, mit den
Blöcken:
Man teile die 8-Menge in {1,2,3,4,5,6} und {7,8} auf. Der erste Block ist klar. Die restlichen Blöcke werden benötigt, um alle restlichen Dreier {x,y,7}, {x,y,8}, {x,7,8} zu erhalten. Weniger als vier Blöcke reichen dazu nicht aus, da die Blöcke mindestens 4 Elemente gemeinsam haben. Man deshalb mit 3 Blöcken nicht mal
Kommen wir jetzt zur Definition des Lotto Designs:
Es sei
![]() .
Ein t-(v,k,p,
.
Ein t-(v,k,p,![]() generalisiertes Covering Design
(engl. general cover) ist ein Tripel (V,
generalisiertes Covering Design
(engl. general cover) ist ein Tripel (V,
![]() ) mit V als
Menge mit v Elementen,
) mit V als
Menge mit v Elementen, ![]() als Mengensystem aller
als Mengensystem aller ![]() p-Untermengen von V und
p-Untermengen von V und ![]() einem Mengensystem von k-Untermengen von V (den sogenannten Blöcken) mit folgender Eigenschaft: Jede p-Untermenge P aus
einem Mengensystem von k-Untermengen von V (den sogenannten Blöcken) mit folgender Eigenschaft: Jede p-Untermenge P aus
![]() hat mit mindestens
hat mit mindestens ![]() Blöcken wenigstens t Elemente
gemein. Ist
Blöcken wenigstens t Elemente
gemein. Ist ![]() spricht man vom (v,k,p,t)-Lotto Design. Die
minimale Blockzahl
spricht man vom (v,k,p,t)-Lotto Design. Die
minimale Blockzahl ![]() bezeichnet die kleinstmögliche Blockzahl des Lotto Designs.
bezeichnet die kleinstmögliche Blockzahl des Lotto Designs.
Bevor wir uns ein Beispiel ansehen, beweisen wir folgenden Satz:
Satz 1: Es seiBeweis: Jede p-elementige Untermenge P von
Beispiel 3: Mit diesem Satz erzeugen wir ein (16,6,5,3)-Lotto Design1 :
Zunächst ist zu bemerken, das (v,k,t,t) Lotto Design ist nichts anders als ein (v,k,t) Covering Design! Mittels Beispiel 2 ist dann auch klar, wie man die 8 Blöcke gewinnt. Nach [2] ist interessanterweise L(16,6,5,3)=7 oder 8 und damit noch eine offene Frage! Ist die minimale Blockzahl noch unbekannt oder verschieden von der Blockzahl, sollte die Blockzahl mitangegeben werden. Etwa so: (16,6,5,3,=8) Lotto Design, 3-(9,6,2,=12) Covering Design.
Anwendung auf Lotto-Systeme
Dazu werden die speziellen Lotto Designs vom Typ (45,6,6,2) und (50,6,6,2) näher untersucht. Um deren minimalen Blockzahlen nach Oben abschätzen zu können, verwenden wir folgenden Satz:
Satz 2:
![]()
Beweis: Wir zerlegen die Menge
![]() in lauter disjunkte Teilmengen
in lauter disjunkte Teilmengen ![]() mit
mit ![]() Elementen. Wählt man eine beliebige
p-Untermenge aus, muss - wegen dem Schubfachprinzip - mindestens ein
Elementen. Wählt man eine beliebige
p-Untermenge aus, muss - wegen dem Schubfachprinzip - mindestens ein ![]() zwei Elemente enthalten.
zwei Elemente enthalten.
![]() ist gerade die kleinste Anzahl von k-Blöcken, um alle Zweier von
ist gerade die kleinste Anzahl von k-Blöcken, um alle Zweier von
![]() mindestens einmal zu überdecken. Da jedes
mindestens einmal zu überdecken. Da jedes ![]() dafür infrage kommt,
folgt daraus die gesuchte Abschätzung.
dafür infrage kommt,
folgt daraus die gesuchte Abschätzung.
Um die oberen Schranken berechnen zu können, greifen wir auf die Tabelle der minimalen Blockzahlen enthalten
in [2] zurück. Auszugsweise sind nur die von uns benötigten C(v,6,2)
für v=6..22 hier wiedergegeben. Die Tabelle lautet:
| v | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| C(v,6,2) | 1 | 3 | 3 | 3 | 4 | 6 | 6 | 7 | 7 | 10 | 10 | 12 | 12 | 15 | 16 | 17 | 19 |
Die Berechnung führt man am besten mit einem CAS wie z.B. MAPLE durch. Die Partitionen von ![]() stehen dort auf Kommando bereit und können mit dem select-Kommando auf solche, die aus genau p-1 Summanden bestehen
und deren Summanden
eine Maximalgröße (hier 22) nicht überschreiten, eingeschränkt werden.
Eine Maximalgröße ist deshalb möglich, weil die mit kleineren Summanden
bereits berechneten Schranken 15 und 19 dann offenbar nicht mehr unterboten
werden können. Die minimalen Blockzahlen sind nämlich mit zunehmenden
stehen dort auf Kommando bereit und können mit dem select-Kommando auf solche, die aus genau p-1 Summanden bestehen
und deren Summanden
eine Maximalgröße (hier 22) nicht überschreiten, eingeschränkt werden.
Eine Maximalgröße ist deshalb möglich, weil die mit kleineren Summanden
bereits berechneten Schranken 15 und 19 dann offenbar nicht mehr unterboten
werden können. Die minimalen Blockzahlen sind nämlich mit zunehmenden ![]() stets monoton nichtfallend. Das CAS liefert als kleinste obere
Schranken:
stets monoton nichtfallend. Das CAS liefert als kleinste obere
Schranken:
L(45,6,6,2)![]() 15=C(9,6,2)+ C(9,6,2)+C(9,6,2)+C(9,6,2)+C(9,6,2),
15=C(9,6,2)+ C(9,6,2)+C(9,6,2)+C(9,6,2)+C(9,6,2),
L(50,6,6,2)![]() 19=C(9,6,2)+ C(9,6,2)+C(9,6,2)+C(9,6,2)+C(14,6,2)
19=C(9,6,2)+ C(9,6,2)+C(9,6,2)+C(9,6,2)+C(14,6,2)
Wenn nun diese Schranken sogar gleich den minimalen Blockzahlen wären, und nicht größer, hätten wir die Blöcke-Konstruktion der Lotto Designs auf kleinere Covering Designs zurückgeführt!
Dies ist tatsächlich der Fall. Die minimalen Blockzahlen L(45,6,6,2)=15 sowie L(50,6,6,2)=L(49,6,6,2)=19 (!!) werden im Artikel von BATE und VAN REES
[1] bewiesen.
Theorem: Auszugsweise entnommen aus [2]:
Die Werte von C(v,k,2) sind bekannt in folgenden Fällen:
1. C(v,k,2) = 3 für 1 < v / k ![]() 3 / 2 ...
3 / 2 ...
5. C(v,k,2) = 7 für 2 < v / k ![]() 7 / 3, außer wenn 3 v = 7 k - 1
7 / 3, außer wenn 3 v = 7 k - 1
Wir benötigen demnach ein Methode die es erlaubt, aus den 3 Blöcken des (3,2,2) Covering Designs die
3 Blöcke des (9,6,2) Covering Designs und aus den 7 Blöcken des (7,3,2) Covering Designs die 7 Blöcke des (14,6,2) Covering Designs zu ermitteln!
Diese Methode wird im Artikel von GORDON, KUPERBERG und PATASHNIK
[3]
erwähnt. Wir betrachten zunächst die folgende Block-Konstruktion eines
![]() -Covering Designs aus d Kopien eines (v,k,2)-Covering Designs :
-Covering Designs aus d Kopien eines (v,k,2)-Covering Designs :
Jedem Block
![]() des (v,k,2)-Covering Designs ordnen wir vermöge Abbildung:
des (v,k,2)-Covering Designs ordnen wir vermöge Abbildung:
![]() genau d Blöcke zu, wobei für die
d-1 hinzukommenden Blöcke
genau d Blöcke zu, wobei für die
d-1 hinzukommenden Blöcke
![]() gelten soll. Alle so gebildeten Blöcke
enthalten, zusammengenommen, genau
gelten soll. Alle so gebildeten Blöcke
enthalten, zusammengenommen, genau ![]() verschiedene Elemente.
Anschließend
vereinigen wir die d-Tupel der eingeführten Blöcke zu einem einzigen neuen
Block mit jeweils genau
verschiedene Elemente.
Anschließend
vereinigen wir die d-Tupel der eingeführten Blöcke zu einem einzigen neuen
Block mit jeweils genau ![]() Elementen.
Wir erhalten so ein Blocksystem mit offenbar
ebensovielen Blöcken wie das Ausgangsdesign. Die Konstruktion beschreibt
letztlich nichts anderes als die Ersetzung eines jeden Elements im Block des
Ausgangsdesigns durch wohlbestimmte d neue Elemente, welche zusammen dann den neuen Block bilden.
Elementen.
Wir erhalten so ein Blocksystem mit offenbar
ebensovielen Blöcken wie das Ausgangsdesign. Die Konstruktion beschreibt
letztlich nichts anderes als die Ersetzung eines jeden Elements im Block des
Ausgangsdesigns durch wohlbestimmte d neue Elemente, welche zusammen dann den neuen Block bilden.
Wir beweisen, dass die Überdeckungseigenschaft für die neuen Blöcke erhalten bleibt!
Satz 3: Es sei d,v![]() 2. Das durch d-fache Ersetzung aus dem (v,k,2)-Covering Designs konstruierte neue Blocksystem, enthält alle Paare aus
2. Das durch d-fache Ersetzung aus dem (v,k,2)-Covering Designs konstruierte neue Blocksystem, enthält alle Paare aus ![]() Elementen, ist also ein
Elementen, ist also ein ![]() -Covering Design.2
-Covering Design.2
Beweis: Wir haben da zum Einen, die durch d-fache Ersetzung jedes Ausgangselementes bedingten ![]() neu hinzukommenden Paare, also
insgesamt
neu hinzukommenden Paare, also
insgesamt
![]() weitere neue Paare im neuen Blocksystem. Zum
Anderen kommen an Stelle von jedem Paar im Block des Ausgangsdesign, jetzt
weitere neue Paare im neuen Blocksystem. Zum
Anderen kommen an Stelle von jedem Paar im Block des Ausgangsdesign, jetzt ![]() weitere neue Paare im neuen Block hinzu, also ingesamt
weitere neue Paare im neuen Block hinzu, also ingesamt
![]() weitere neue Paare. Das ergibt folgende Anzahl verschiedener Paare:
weitere neue Paare. Das ergibt folgende Anzahl verschiedener Paare:
Jedes denkbare Paar gebildet, aus den
Folgerung1: Sei ![]() und
und
![]() (oder: v / k = v' / k'), dann gilt
(oder: v / k = v' / k'), dann gilt
![]() .
.
Folgerung2: Aus Symmetriegründen folgt Identität:
![]()
Beispiel 4: Wegen
![]() ist das (25,3,2)-Covering Design sogar ein Steiner-Tripelsystem mit
ist das (25,3,2)-Covering Design sogar ein Steiner-Tripelsystem mit
![]() und b =
und b =
![]() Blöcken. Mit Erweiterungsfaktor d=2 erhalten
wir daraus ein (50,6,2,=100)-Covering Design. Es ist also einerseits
C(50,6,2)=L(50,6,2,2)
Blöcken. Mit Erweiterungsfaktor d=2 erhalten
wir daraus ein (50,6,2,=100)-Covering Design. Es ist also einerseits
C(50,6,2)=L(50,6,2,2)![]() 100
andererseits aber L(50,6,6,2)=19. Ersteres überdeckt
100
andererseits aber L(50,6,6,2)=19. Ersteres überdeckt
Blöcke für (45,6,6,2) und (50,6,6,2) Lotto Designs
Mit der Erweiterungsmethode konstruiert man nun leicht, aus dem
(3,2,2)-Covering Design (einem trivialen Steiner-System, darstellbar durch
ein Dreieck):
mittels Erweiterungsfaktor d=3, ein (9,6,2)-Covering Design :
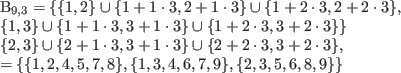
und aus dem (7,3,2)-Covering Design (einem Steiner-Tripelsystem, darstellbar durch eine FANO-Ebene):
mittels Erweiterungsfaktor d=2, ein (14,6,2)-Covering Design :
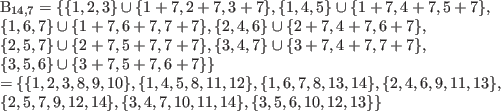
Aus
Natürlich kann man alternativ, die Blöcke zum (9,6,2) und (14,6,2) Covering Design auch über die Website von
LA JOLLA : http://www.ccrwest.org/cover/table.html oder gleich das (49,6,6,2) Lotto Design über die Website : http://www.weefs-lottosysteme.de direkt entnehmen. Wer hingegen ein eigenes Lottodesign erwägt, schaue mal vorbei unter: http://lottoarchitect.anastasios-tampakis.net
Abschließend noch eine Warnung vor einem Trugschluss, der so lautet:
Mit dem hier abgeleiteten Tippsystem hat man ja garantiert 2 Richtige. Also
braucht es nur noch einen - mit bedingter Wahrscheinlichkeit - eintretenden
dritten Treffer zum Gewinn!.
Leider ist das falsch, denn 2 Richtige
sind erst nach der Ziehung der 6.ten Gewinnzahl garantiert. Weitere Richtige kann es danach aber nicht mehr geben - ausgenommen die Superzahl natuerlich. Die dafür ebenfalls infrage kommende Zusatzzahl von 6aus45, führt hingegen allein noch nicht zum Gewinn.
In Hinblick auf die mittlere Gewinnerwartung, bringen
Systemspiele keinerlei Vorteile gegenüber gleichvielen
zufälligen
Einzeltipps. Anders sieht es dagegen mit der Wahrscheinlichkeit überhaupt etwas zu gewinnen aus. Bei Wahl eines der offiziellen Lotto-Systemspiele, ist die Gewinnchance sogar signifikant schlechter! Aber auch bei den hier betrachteten Lotto Designs von 6aus45 und 6aus49 ist sie oft nur vergleichbar mit der gleichvieler Zufallstipps!